Logan Liu's Blog
0%

Glow-TTS

摘要

之前的非自回归模型在训练时往往需要额外的对齐知识（如fastspeech先蒸馏出一个duration predictor，fastspeech2使用MFA工具），而在本文中使用Flow和动态规划搜索最可能的文本与语音表示之间的单调对齐(monotonic alignment)路径。最终的结果表明这种强制单调硬对齐(enforcing hard)可以使TTS更加鲁棒，而Flow的使用可以使合成的语音更快、多样(diverse)以及可控(controllable)。此外，在合成质量差不多的情况下，Glow-TTS的生成速度比自回归的Tacotron2快了一个数量级。

前置知识

  • 非自回归(Non AutoRegressive, NAR)TTS与自回归(AutoRegressive, AR)TTS的区别在于AR TTS在合成语音时需要step by step，合成速度较慢。而AR TTS可以parallel生成。
  • Flow Model：可以将一个简单的分布变成一个复杂的分布。
  • FastSpeech先蒸馏出一个duration predictor得到文本与语音帧的对齐关系，FastSpeech2使用MFA工具得到文本与语音帧的对齐关系。本文通过单调对齐搜索(MAS)找到对齐关系。
  • WaveGlow、FloWaveNet都是早于该项工作将Flow用于TTS，但是是用于vocoder建模；而本文用于acoustic model。在此之前也有Flowtron、Flow-TTS等工作将Flow用于acoustic model建模，但是都是进行soft attention alignment，与本文的hard monotonic alignment有所不同。

模型

Glow-TTS训练与推理流程

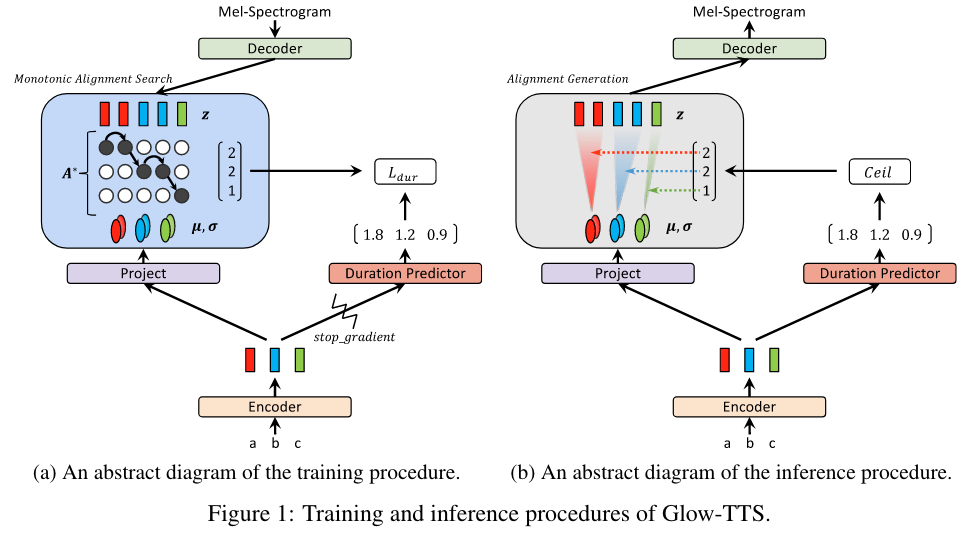
训练与推理过程

训练过程

Glow-TTS通过flow-based decoder $f_{dec}:z\rightarrow x$ 转换先验条件分布$P_Z(z|c)$ 从而完成对梅尔谱的条件分布(conditional distribution) $P_X(x|c)$ 的建模，通过换元法，我们可以精确计算$P_X(x|c)$ 的似然函数：

$$
\operatorname{log}P_X(x|c)=\operatorname{log}P_Z(z|c)+\operatorname{log} \left|\operatorname{dec} \frac{\partial f^{-1}_{dec}(x)}{\partial x}\right|
$$

我们可以用对齐函数(alignment function) $A$ 以及神经网络 (text encoder) 参数 $\theta$ 参数化先验分布$P_Z(z|c)=P_Z(z|c;\theta,A)$ 。text encoder将 text condition $c=c_{1:T_{text}}$ 映射为多元高斯分布的统计量 $\mu=\mu_{1:T_{text}}$ 和 $\sigma=\sigma_{1:T_{text}}$，其中 $T_{text}$ 表示文本输入的长度。而对齐函数 $A$ 将多元高斯分布的统计量映射为语音的潜在表示 $z$ 。我们假设对齐函数是单调和满射(surjective)的，以保证不会跳过或者重复文本输入。所以先验分布 $P_Z(z|c)$可以用如下表示：

$$
\operatorname{log} P_Z(z|c;\theta,A) = \sum^{T_{mel}}_{j=1}\operatorname{log} \mathcal{N}(z_j;\mu_{A(j)},\sigma_{A(j)})
$$

$T_{mel}$ 表示输入的梅尔谱的长度。

这样我们的目标就转换成求对齐 $A$ 以及参数 $\theta$ 以最大化数据的似然函数，如下式：

$$
\begin{aligned} \operatorname{max}_{\theta,A} L(\theta, A) &= \operatorname{max}_{\theta,A} \operatorname{log} P_X (x|c; A, \theta) \\ &=\operatorname{max}_{\theta,A}(\sum^{T_{mel}}_{j=1}\operatorname{log} \mathcal{N}(z_j;\mu_{A(j)},\sigma_{A(j)})+\operatorname{log} \left|\operatorname{dec} \frac{\partial f^{-1}_{dec}(x)}{\partial x}\right|) \end{aligned}
$$

但是该公式的求解是intractable的（类似VAE），为了克服intractability的问题，我们降低参数的搜索空间，并将对齐问题分解为两个子步骤：(i) 用现在的参数 $\theta$ 以及下式搜索出最可能的单调对齐路径 $A^*$，单调对齐搜索将在下个小节进行介绍 (ii) 更新参数 $\theta$ 以最大化对数似然 $P_X(x|c; A^*,\theta)$ 。

$$
A^* = \operatorname{arg}\operatorname{max}_{A} \operatorname{log} P_X (x|c; A, \theta) = \operatorname{arg} \operatorname{max}_{A}\sum^{T_{mel}}_{j=1}\operatorname{log} \mathcal{N}(z_j\mu_{A(j)},\sigma_{A(j)})
$$

虽然修改后的目标函数不能保证优化到 $\operatorname{max} _{\theta,A} L(\theta, A)$ 的全局最优，但仍提供了一个好的下界（good lower bound）。

推理过程

为了在推理时也能得到最可能的单调对齐路径 $A^*$ ，我们也训练了一个时长预测器(duration predictor) $f_{dur}$去拟合从 $A^*$ 中得到的时长标签，从$A^*$ 中得到的时长标签的公式如下式：

$$
d_i = \sum^{T_{mel}}_{j=1}1_{A^*(j)=i}, i = 1,\ldots,T_{text}
$$

duration predictor的训练过程使用MSE loss计算损失：

$$
L_{dur} = MSE(f_{dur}(sg[f_{enc}(c)]),d)
$$

推理过程中分别使用text encoder和duration predictor得到先验分布的统计量 $\mu$ 和 $\sigma$ 以及对齐 $A$，然后从先验分布中采样出一个隐变量，再通过flow-based decoder合成梅尔谱。

单调对齐搜索

MAS用于搜索输入语音（实际是从梅尔谱 $x$ 得到的隐变量 $z$ ）和文本（实际是从text encoder得到的先验分布统计量 $\mu$ 和 $\sigma$ ）之间的对齐。

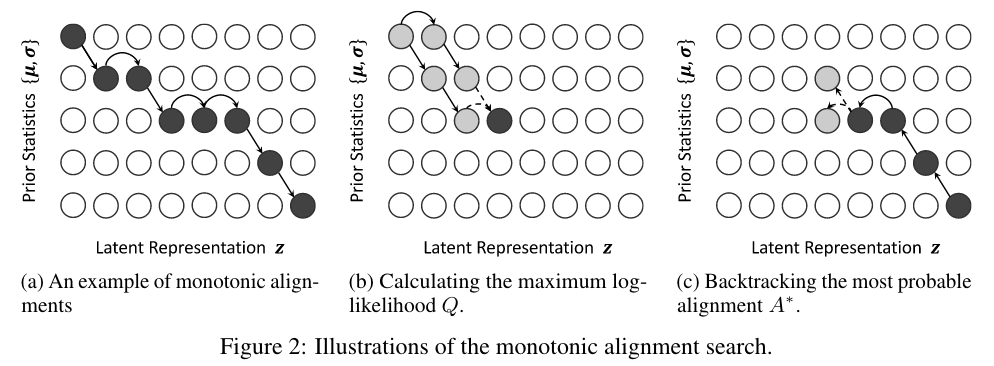
对齐 $A^*$ 是通过递归的方式求得的，伪代码如下图所示，其中 $Q_{i,j}$ 表示 $\mu$ 和 $\sigma$ 的前 $i$ 个元素和 $z$ 的前 $j$ 个元素的最大对数似然（maximum log-likehood），因为对齐符合单调性(monotonic)和满射性(surjection)，所以 $Q_{i,j}$ 可以以递归的方式从 $Q_{i-1,j-1}$和 $Q_{i,j-1}$ 获得，从而大大节省了搜索对齐的时间。

$$
\begin{aligned}Q_{i,j}=\operatorname{max}_{A}\sum_{k=1}^j \operatorname{log} \mathcal{N}(z_k;\mu_{A(k)},\sigma_{A(k)})\\ =\operatorname{max}(Q_{i-1,j-1},Q_{i,j-1}) + \operatorname{log} \mathcal{N}(z_j;\mu_{i},\sigma_{i})\end{aligned}
$$

找到最终的 $Q_{T_{text},T_{mel}}$ 之后，可以通过回溯找到对齐路径；

模型架构

Decoder

flow-based decoder是Glow-TTS的核心。训练阶段我们需要将梅尔谱转换为潜在表示以便进行最大似然估计和对齐搜索。而在推理阶段，我们需要将先验分布变为梅尔谱的分布以便进行高效的并行解码。而flow-based模型符合我们不同阶段都可以并行的需求。具体地，我们的block由多个块(block)组成，每个block都是由activation normalization layer, invertible 1x1 convolution layer, and affine coupling layer组成，affine coupling layer和WaveGlow中的相同。

为了计算更加高效，在flow之前将80维的梅尔谱组合成160维的特征图(feature map),如下图(b)，其中前80维是serve的，后80维是要进行scale和translate的。在进行卷积核大小为4的1x1卷积之前，会将160维的特征图分为40组(160=4*40)。为了让每个group都有affine coupling layer的”可变”(scale and translated)与”不变”(serve)两部分，以保证能由小的 $\operatorname{det}(M)$ 得到整个flow模型的 $\operatorname{det}(M)$ 的正确性（见推导），所以会进行Channel Mixing（图c的左边）。

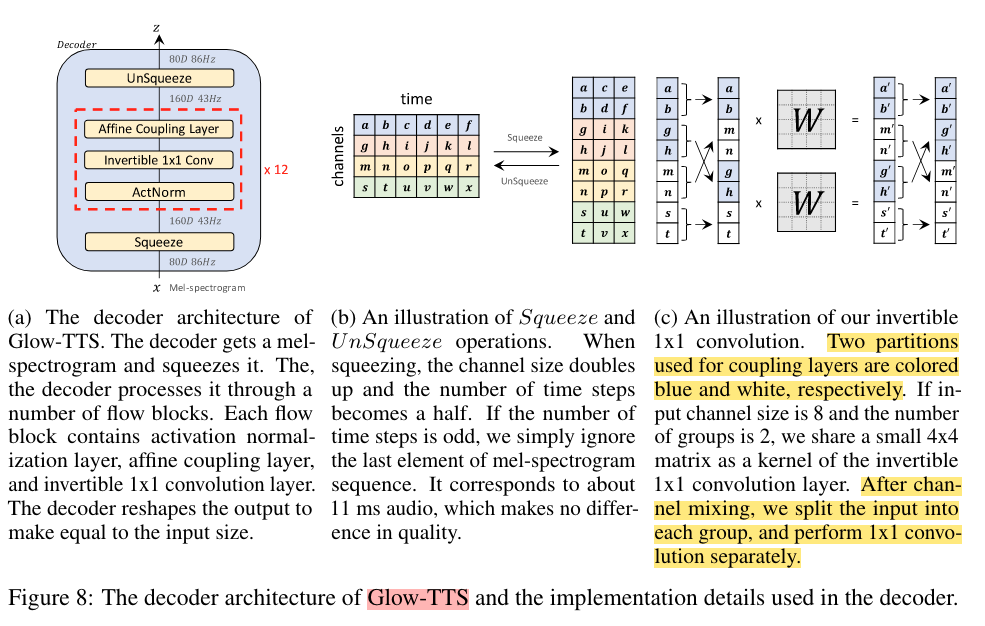
invertible 1x1 convolution包含三个子步骤，如上图c所示：

  1. Allow Channel Mixing In Each Group（图c的左边）
  2. 1x1 convolution （图c的中间）
  3. Reverse Channel Mixing（图c的右边）

其对应的代码如下所示：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
# To Allow Channel Mixing In Each Group（图c的左边，Two partitions used for 
# coupling layers are colored blue and white, respectively）
x = x.view(b, 2, c // self.n_split, self.n_split // 2, t)
x = x.permute(0, 1, 3, 2, 4).contiguous().view(b, self.n_split, c // self.n_split, t)

# 1x1 convolution （图c的中间）
if reverse:
  if hasattr(self, "weight_inv"):
    weight = self.weight_inv
  else:
    weight = torch.inverse(self.weight.float()).to(dtype=self.weight.dtype)
  logdet = None
else:
  weight = self.weight
  if self.no_jacobian:
    logdet = 0
  else:
    logdet = torch.logdet(self.weight) * (c / self.n_split) * x_len # [b]

weight = weight.view(self.n_split, self.n_split, 1, 1)
z = F.conv2d(x, weight)

# Reverse Channel Mixing（图c的右边）
z = z.view(b, 2, self.n_split // 2, c // self.n_split, t)
z = z.permute(0, 1, 3, 2, 4).contiguous().view(b, c, t) * x_mask

根据Glow中1x1卷积中weight的要求，要求weight是正交矩阵，其对应的代码为

1
2
3
4
5
# torch.qr将一个矩阵分解为一个正交矩阵与一个上三角矩阵的乘积，其中的第一个部分是正交矩阵。
w_init = torch.qr(torch.FloatTensor(self.n_split, self.n_split).normal_())[0]
if torch.det(w_init) < 0:
  w_init[:,0] = -1 * w_init[:,0]
self.weight = nn.Parameter(w_init)

Encoder and Duration Predictor

encoder的结构与transformer TTS相同，为了得到先验分布的统计量 $\mu$ 和 $\sigma$ ，在encoder的尾部添加了一个线性映射层。dutation preictor是由两个卷积层、ReLU激活函数接一个线性映射层组成，和FastSpeech一致。

实验

为了验证方法的有效性，在两个数据集上进行验证：单说话人和多说话人。单说话人使用LJSpeech数据集，其包含13100条语音，（12500条用来训练，100条用于验证，500条用于测试）。多说话人上使用LibriTTS数据集的train-clean-100，包含247个说话人，总共54小时。数据处理过程中会对所有音频开头和结尾的静音段去掉，并且会去掉文本长度超过190的音频（29181条用来训练、88用来验证、442用来测试）。此外，集外测试集使用227条来自Harry Potter and the Philosopher’s Stone的文本进行，最大长度超过800。

base模型选择Tacotron2，vocoder使用WaveGlow，建模单元为音素(phoneme)。

训练的过程中我们设置先验分布的标准差 $\sigma$ 为常量1，Adam作为optimizer，Noam作为learning rate scheduler，使用两张V100混合精度训练3天，迭代240K步。

为了训练多说话人的 Glow-TTS 模型，speaker embedding 被用在 flow-based 的 decoder 以及 text encoder上，对应的代码如下所示：

1
2
3
# encoder为text encoder、decoder为flow-based decoder，x为文本输入，y为梅尔谱输入，g为说话人embedding
x_m, x_logs, logw, x_mask = self.encoder(x, x_lengths, g=g)
z, logdet = self.decoder(y, z_mask, g=g, reverse=False)

结果

音频质量

音频质量使用 MOS (mean opinion score) 作为评价指标，随机从测试集得到 50 段音频然后使用 Amazon Mechanical Turk 工具获得 MOS 值，结果如下：

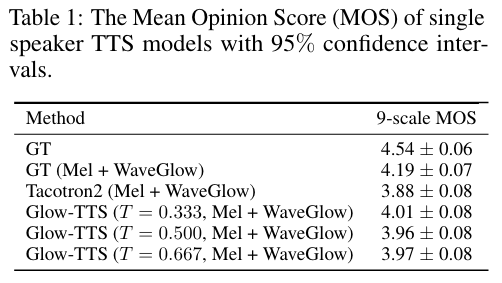
测试时会变换不同的 standard deviation (i.e., temperature T)分别得到 MOS值，结果表明当temperature 设置为 0.333 时 MOS值最高，均好于Tacotron 2的表现。

采样速度和鲁棒性

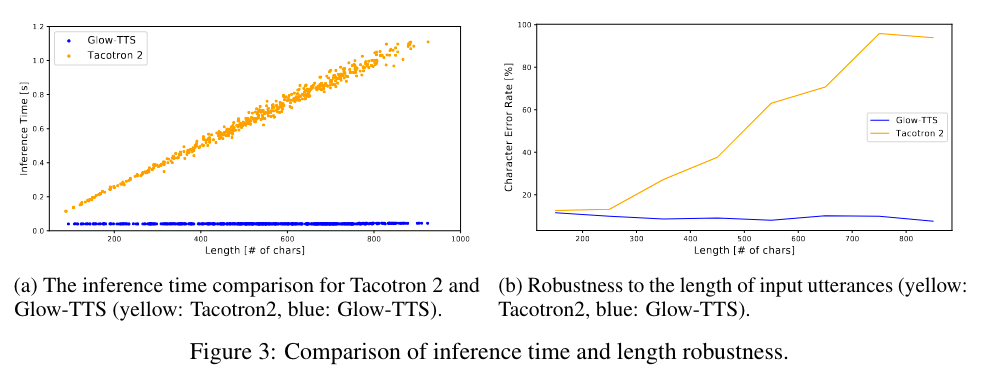
采样速度 (Sampling Speed)：如上图所示，因为 Glow-TTS 是非自回归模型，所以其生成 mel-spectrogram 的时间与其文本的长度无关 (40ms)，而 Tacotron 2模型与所要生成的文本长度线性相关。使用 Glow-TTS生成 1 分钟的音频所需的时间为 1.5s，其中vocoder占用了 95% 的时间，而 Glow-TTS 只占用了其中的 5% (55ms), 几乎是可以忽略不计的。

鲁棒性 (Robustness)：Glow-TTS 对长音频的合成具有很强的鲁棒性，如上图(b)，当使用Harry Potter and the Philosopher’s Stone中的长文本作为测试集时，Tacotron 2合成的音频的 CER 随文本长度的升高显著上升，而 Glow-TTS 几乎保持不变。

多样性和可控性

通过 $f_{dec}(z)$ 可以将采样出的潜在表示 $z$ 合成梅尔谱，而 $z \sim \mathcal{N}(\mu, T)$ 是通过如下公式得到：

$$
z = \mu + \epsilon * T
$$

其中 $\epsilon$ 表示从标准正态分布进行采样的一个样本， $\mu$ 和 $T$ 是先验分布的均值和标准差。以下从几个方面说明 Glow-TTS 的可控性：

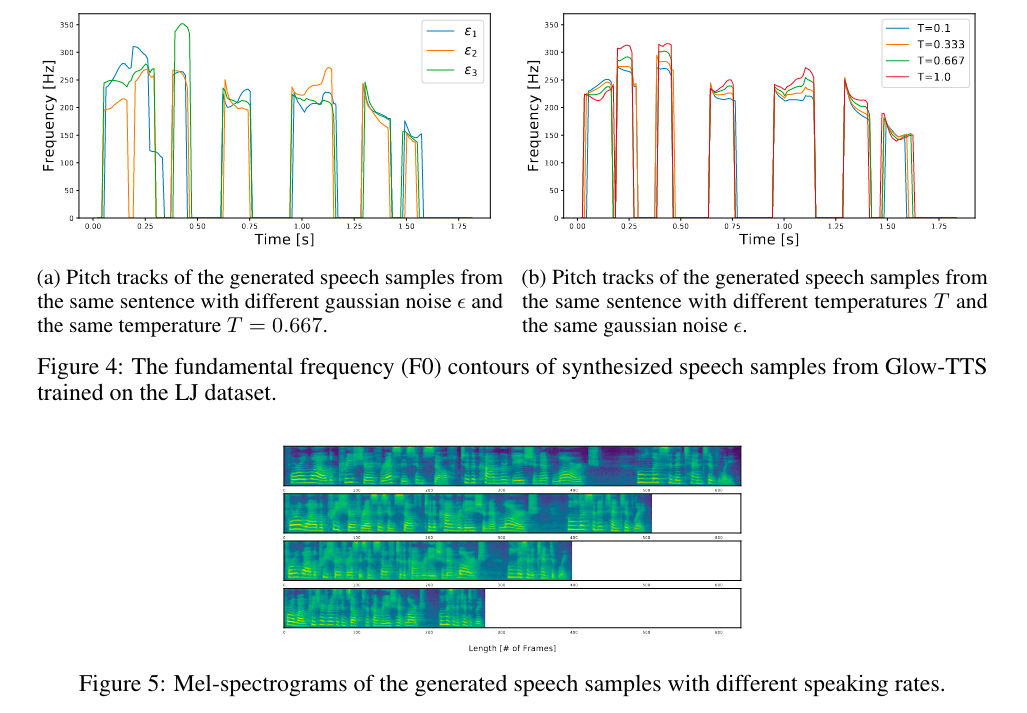
  • 重音和语调 (strss and intonation): 如图(a)，通过改变 $\epsilon$ 可以控制重音和语调；
  • 音高 (pitch): 如图(b)，可以通过改变 $T$ 进行控制；
  • 语速 (speaking rate)：可以让duration preditor 乘上不同的值进行控制；

Multi-Speaker TTS

将从 Audio Quality、Speaker-Dependent Duration、Voice Conversion几个方向进行评估。

音频质量：从 50 个说话人中挑选出 50 段音频得到 MOS 值，结果如下，可见Glow-TTS具有更好的音频质量。

Speaker-Dependent Duration：不同说话人对相同token预测的时长如下图，可见对不同说话人相同token所预测的时长具有很大的区分性，说明提出的模型具有Speaker-Dependent Duration。

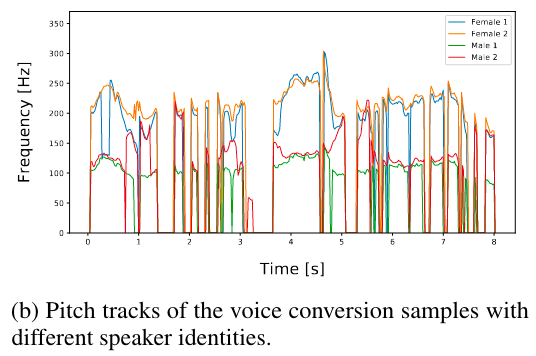
声音转换：因为 Glow-TTS 会对潜在表征 $z$ 和说话人进行解耦（因为在训练的时候没有提供说话人信息给 encoder ），所以可以用来进行声音转换，为了测试这种解耦的程度，本文把 Ground Truth 梅尔谱 $x$ 和说话人信息 $s$ 转换成潜在表示 $z$ ，即 $z=f^{-1}_{dec}(x|s)$ ，然后提供另外一个说话人的信息用于合成新的梅尔谱，即 $\hat{x}=f_{dec}(z|\hat{s})$，然后分别得到 $x$ 和 $\hat{x}$ 的 pitch 图，如下图所示，不同说话人的 pitch 有很大的区分性，但趋势是相同的，说明该模型能完成潜在表征 $z$ 和说话人信息的解耦。

疑问

  1. stop gradient的作用是什么？

训练时可以通过单调对齐搜索得到spectrogram和text的对齐关系，并可以通过不断迭代获取更好的对齐，完全可以不用Duration Predictor的参与。但是在推理时并没有可以参考的spectrogram，所以训练时“顺带”训了一个Duration Predictor模块以便推理时可以得到对齐关系，以便从text表示中生成spectrogram。

参考

  1. https://github.com/jaywalnut310/glow-tts
  2. https://arxiv.org/abs/2005.11129
  3. https://loganliu66.github.io/FlowModel/