Flow Model

摘要

GAN和VAE都没有显式地（explicitly）对真实数据的概率密度函数（probability density function，PDF） $p(\mathbf{x}),\mathbf{x}\in\mathcal{D}$ 进行建模，而是采用对抗训练或优化上界（Evidence Lower Bound，ELBO）的方式避开概率计算，因为 $p(\mathbf{x})$太难算了！以带隐变量的生成模型 $p(\mathbf{x})=\int p(\mathbf{x}\mid\mathbf{z})p(\mathbf{z})d\mathbf{z}$ 为例，因为不可能遍历所有的潜在编码 $\mathbf{z}$，所以 $p(\mathbf{x})$的计算是非常困难的（intractable）。

Flow-based生成模型通过normalizing flows解决了这个问题，normalizing flows是一个非常强大的概率密度函数计算工具。计算出 $p(\mathbf{x})$之后我们可以有效地完成下游任务，如：采样出不存在于训练集但真实存在的样本点（data generation）、计算某个时间可能发生的概率（density estimation）等等。

线性代数基础概述

在flow-based模型之前，先来了解线性代数中两个重要的概念：雅可比行列式（Jacobian Determinant）与变量变换定理/换元积分法（the change of variable rule）；前者阐述了雅可比行列式的定义，后者阐述了如何用雅可比行列式进行变量变换；

雅可比矩阵和行列式

如果一个函数 $\mathbf{f}$把一个n维的输入映射为m维的输出， $\mathbf{f}: \mathbb{R}^n\mapsto\mathbb{R}^m$，那么这个函数的一阶（first-order）偏导数（partial derivative）叫做雅可比矩阵（Jacobian Matrix），表示为 $\mathbf{J}$。 $\mathbf{J}$的第i行、第j列的计算公式为 $\mathbf{J_{ij}=\frac{\partial{f_i}}{\partial{x_j}}}$

$$
\mathbf{J}=\left[\begin{array}{ccc}\frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n}\end{array}\right]
$$

雅可比行列式只存在于方阵（square matrices）中，是一个由矩阵中所有元素参与计算得到的实数；行列式的绝对值表示在该数据点处对空间扩展和收缩的程度（how much expands or contracts space），也可以理解为行列式中的行或列向量所构成的超平行多面体的有向面积或有向体积。对于二阶行列式：

$$
\left[\begin{array}{cc} a_1 & a_2 \\ b_1 &b_2\end{array} \right]=a_1b_2-a_2b_1
$$

例如向量 $a=[1,0], b=[0,1]$所构成的有向面积为1*1-0*0=1。而对于雅可比矩阵，对应函数 $\mathbf{f}$在点 $\mathbf{x}$的微分，矩阵的每一项代表各个维度下面积或体积的伸缩因子。

将上面二阶行列式的计算扩展到n阶有如下公式：

$$
\operatorname{det} M=\operatorname{det}\left[\begin{array}{cccc}a_{11} & a_{12} & \ldots & a_{1 n} \\ a_{21} & a_{22} & \ldots & a_{2 n} \\ \vdots & \vdots & & \vdots \\ a_{n 1} & a_{n 2} & \ldots & a_{n n}\end{array}\right]=\sum_{j_1 j 2 \ldots j_n}(-1)^{\tau\left(j_1 j_2 \ldots j_n\right)} a_{1 j_1} a_{2 j_2} \ldots a_{n j_n}
$$

其中 $j_1j_2…j_n$是 $1,2,…,n$的一个排列， $\sum\limits_{j_1 j_2 \ldots j_n}$是遍历所有 $1,2,…,n$排列 ${j_1 j_2 \ldots j_n}$求和；方阵 $M$的行列式有如下性质：

如果 $\operatorname{det}(M)=0$，则矩阵 $M$不可逆，否则矩阵可逆；
行列式的乘积等于矩阵乘积的行列式 $\operatorname{det}(AB)=\operatorname{det}(A)\operatorname{det}(B)$；（证明）

变量变换定理(Change of Variable Theorem)

给定一维随机变量$z$以及概率密度函数 $z\sim\pi(z)$,我们使用映射函数构建一个新的随机变量 $x=f(z)$,函数 $f$是可逆的，所以有 $z=f^{-1}(x)$, 如何得到新的随机变量 $x$的概率密度函数 $p(x)$呢? 由概率分布的定义可知：

$$
\int p(x)dx = \int \pi(z)dz = 1 \
\therefore p(x)=\pi(z)\left|\frac{dz}{dx}\right|=\pi(f^{-1}(x))\left|\frac{df^{-1}}{dx}\right|=\pi(f^{-1}(x))\left|(f^{-1})'(x)\right|
$$

根据定义， $\int\pi(z)dz$是无限（infinite）多个宽度无穷小（infinitesimal）的矩形面积之和，在位置 $z$处的矩形的高度就是其密度函数 $\pi(z)$。由 $z=f^{-1}(x)$可得 $\frac{\Delta z}{\Delta x}=(f^{-1}(x))‘$, $\Delta z=(f^{-1}(x))’ \Delta x$, 所以此处的 $(f^{-1}(x))'$ 可以任务是变量 $x$和 $z$在两个不同的坐标系中对应位置处的矩形的面积的比值。

多维变量的变换与一维变量的变换比较相似：

$$
\begin{aligned}\mathbf{z} & \sim \pi(\mathbf{z}), \mathbf{x}=f(\mathbf{z}), \mathbf{z}=f^{-1}(\mathbf{x}) \\ p(\mathbf{x}) & =\pi(\mathbf{z})\left|\operatorname{det} \frac{d \mathbf{z}}{d \mathbf{x}}\right|=\pi\left(f^{-1}(\mathbf{x})\right)\left|\operatorname{det} \frac{d f^{-1}}{d \mathbf{x}}\right|\end{aligned}
$$

其中， $\operatorname{det} \frac{d f^{-1}}{d \mathbf{x}}$是函数 $f$的雅可比行列式。

实例

https://www.gwylab.com/note-flow_based_model.html

Normalizing Flows

数学原理影响我们对模型的选择

密度估计（density estimation）在很多机器学习问题上都有应用，但一个好的密度估计又很难做到。例如，由于深度学习中需要进行反向传播，所以我们希望后验概率分布（posterior， $p(z|x)$）尽可能的简单，以方便求导。这也是为什么隐变量生成模型（latent variable generative model），如VAE，中通常使用高斯分布，尽管现实世界中分布往往比高斯分布更复杂。

Normalizing Flow模型可以很好的进行分布估计（distribution approximation），normalizing flow可以通过一系列的可逆变换函数将一个简单的分布变成复杂的分布。利用变量变化定理，可以反复的替换其中一部分变量，直到得到一个新的概率分布。

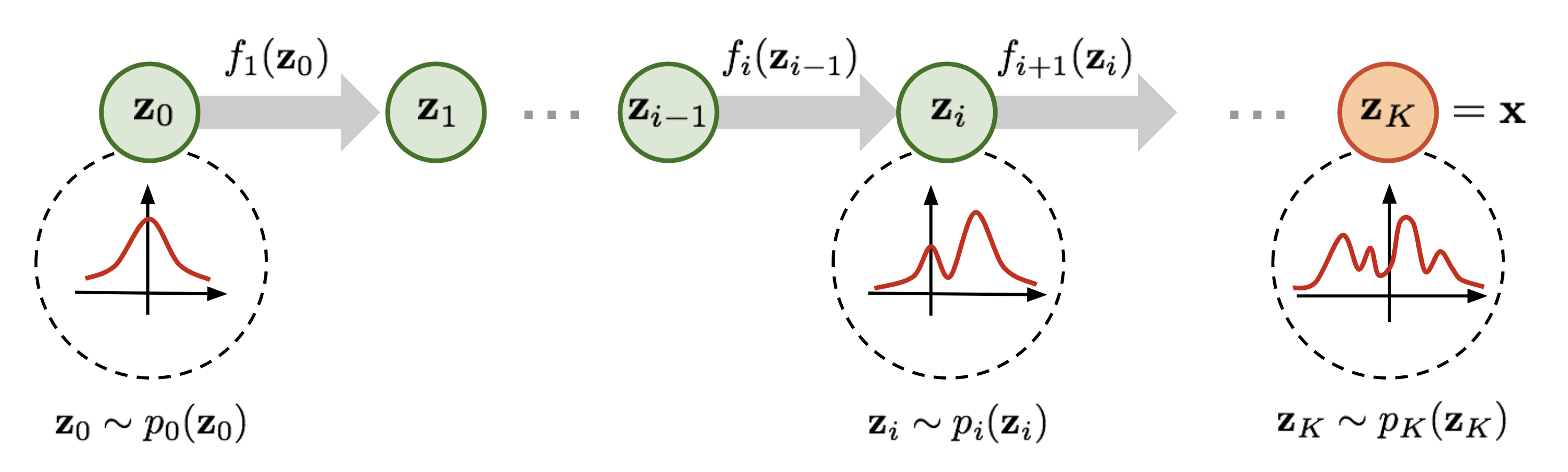
图1. Normalizing Flow模型变换示意图，将一个简单的分布 $p_0(z_0)$逐步替换成一个复杂的分布 $p_K(z_K)$

根据图1我们有

$$
\begin{aligned}\mathbf z_{i-1}&\sim p_{i-1}(\mathbf z_{i-1}) \\ \mathbf z_{i} &= f_{i}(\mathbf z_{i-1}), thus \\ \mathbf z_{i-1} &= f^{-1}_{i}(\mathbf z_{i}) \end{aligned}
$$

根据多维变量的变换定律有：

$$
\begin{aligned} p_i(\mathbf z_i)&=p_{i-1}(\mathbf z_{i-1})\left|\operatorname{det}\frac{d \mathbf z_{i-1}}{d \mathbf z_{i}}\right| \\ &=p_{i-1}(\mathbf z_{i-1})\left|\left(\operatorname{det}\frac{d \mathbf z_{i}}{d \mathbf z_{i-1}}\right)^{-1}\right| \\ &=p_{i-1}(\mathbf z_{i-1})\left|\left(\operatorname{det}\frac{d f_{i}(\mathbf z_{i-1})}{d \mathbf z_{i-1}}\right)^{-1}\right|;反函数定理 \\ &=p_{i-1}(\mathbf z_{i-1})\left|\operatorname{det}\frac{d f_{i}(\mathbf z_{i-1})}{d \mathbf z_{i-1}}\right|^{-1};雅可比行列式的反函数性质 \end{aligned}
$$

所以有：

$$
log(p_i(\mathbf z_i))=log(p_{i-1}(\mathbf z_{i-1})) - log\left|\operatorname{det}\frac{d f_{i}(\mathbf z_{i-1})}{d \mathbf z_{i-1}}\right|
$$

给定这样一连串的概率密度函数，我们知道每两个连续的变量之间的关系，从而可以知道初始分布 $z_0$与输出 $x$之间的转换公式：

$$
\begin{aligned}\mathbf{x}=\mathbf{z}_K & =f_K \circ f_{K-1} \circ \cdots \circ f_1\left(\mathbf{z}_0\right) \\ \log p(\mathbf{x})=\log \pi_K\left(\mathbf{z}_K\right) & =\log \pi_{K-1}\left(\mathbf{z}_{K-1}\right)-\log \left|\operatorname{det} \frac{d f_K}{d \mathbf{z}_{K-1}}\right| \\ & =\log \pi_{K-2}\left(\mathbf{z}_{K-2}\right)-\log \left|\operatorname{det} \frac{d f_{K-1}}{d \mathbf{z}_{K-2}}\right|-\log \left|\operatorname{det} \frac{d f_K}{d \mathbf{z}_{K-1}}\right| \\ & =\ldots \\ & =\log \pi_0\left(\mathbf{z}_0\right)-\sum_{i=1}^K \log \left|\operatorname{det} \frac{d f_i}{d \mathbf{z}_{i-1}}\right|\end{aligned}
$$

随机变量经过的路径 $z_i=f_i(z_{i-1})$就是flow，连续分布 $\pi_i$形成的完整链路就是normalizing flow。上述公式成立，需要变换函数 $f_i$ 满足如下条件：

可逆
雅可比行列式容易计算

工程实现

有了normalizing flow的数学原理，我们看在工程上如何实现它，尤其是神经网络应用在何处。

RealNVP

RealNVP通过叠加一系列可逆的对射变换函数（bijective transformation function）实现normalizing flow。每个对射函数 $f:x\mapsto y$,被称为仿射耦合层（affine coupling layer），它把输入的维度分成两部分：

前 $d$ 维保持不变；
第 $d+1$至 $D$维，执行仿射变换（“scale-and-shift”），放缩(scale)和移动(shift)的参数都是以前 $d$ 维作为输入的函数；

$$
\begin{array}{cc} \mathbf y_{1:d}=\mathbf x_{1:d} \\
\mathbf y_{d+1:D}=\mathbf x_{d+1:D}\odot \operatorname{exp}(s(\mathbf x_{1:d})) + t(\mathbf x_{1:d}) \end{array}
$$

其中 $s(\cdot)$和 $t(\cdot)$是scale和translation函数，这两个函数将 $\mathbb{R^d}$映射为 $\mathbb{R^{D-d}}$, $\odot$是逐元素相乘。下面让我们验证这种变换是否满足上述两个条件；

条件1: 可逆

可逆比较容易证明，如下：

$$
\begin{cases}\begin{array}{ll} \mathbf { y } _ { 1 : d } = \mathbf { x } _ { 1 : d } \\ \mathbf { y } _ { d + 1 : D } = \mathbf { x } _ { d + 1 : D } \odot \operatorname { e x p } ( s ( \mathbf { x } _ { 1 : d } ) ) + t ( \mathbf { x } _ { 1 : d } ) \end{array} \end{cases} \Leftrightarrow \begin{cases}\begin{array}{ll} \mathbf { x } _ { 1 : d } = \mathbf { y } _ { 1 : d } \\ \mathbf { x } _ { d + 1 : D } = (\mathbf { y } _ { d + 1 : D } - t ( \mathbf { y } _ { 1 : d } )) \odot \operatorname { e x p } ( -s ( \mathbf { y } _ { 1 : d } ) )\end{array} \end{cases}
$$

条件2: 雅可比行列式比较容易计算

上述变换函数的雅可比行列式如下所示，是一个下三角矩阵：

$$
\mathbf{J} = \left[\begin{array}{cc}\mathbb{I} & \mathbb{0}_{d\times(D-d)} \\
\frac{\partial \mathbf{y}_{d+1: D}}{\partial \mathbf{x}_{1: d}} & \operatorname{diag}(\operatorname{exp}(s(\mathbf x_{1:d})))\end{array}\right]
$$

下三角矩阵的行列式为（三角阵的行列式等于对角线元素之积）：

$$
\operatorname{det}(\mathbf{J})=\prod_{j=1}^{D-d} \exp \left(s\left(\mathbf{x}_{1: d}\right)\right)_j=\exp \left(\sum_{j=1}^{D-d} s\left(\mathbf{x}_{1: d}\right)_j\right)
$$

以上证明了RealNVP满足可逆和雅可比行列式容易计算两个条件。此外，由条件1的证明可知计算 $f^{-1}$不需要计算 $s$和 $t$的逆函数，雅可比行列式的计算也不需要计算 $s$和 $t$的行列式，所以 $s$和 $t$可以是任意复杂度，比如 $s$和 $t$均可以是一个神经网络。

在一个仿射耦合层（affine coupling layer）中，某些纬度是保持不变的，这会导致生成数据中总有一片区域看起来像固定的图样。为了保证所有维度都有被替换的机会，会不断的交换复制模块（copy）与仿射模块（affine）的顺序，这样最终的生成图像就不会包含完全copy自初始图像的部分。

NICE

NICE（Non-linear Independent Component Estimation）是RealNVP的先导工作，与RealNVP不同的是NICE是不包含缩放（scale）项的仿射耦合层，也称加性（additive）耦合层。

$$
\begin{cases}\begin{array} { l l } { \mathbf { y } _ { 1 : d } } { = \mathbf { x } _ { 1 : d } } \\ { \mathbf { y } _ { d + 1 : D } } { = \mathbf { x } _ { d + 1 : D } + m ( \mathbf { x } _ { 1 : d } ) }\end{array} \end{cases} \Leftrightarrow \begin{cases} \begin{array}{ll}\mathbf{x}_{1: d} =\mathbf{y}_{1: d} \\ \mathbf{x}_{d+1: D} =\mathbf{y}_{d+1: D}-m\left(\mathbf{y}_{1: d}\right)\end{array} \end{cases}
$$

Glow

Glow模型扩展之前的可逆生成模型，如NICE、RealNVP，这些模型在像素维度上进行划分，执行仿射对偶变换。而Glow在通道（channel）维度上进行copy和affine，在每次耦合变换中按顺序选择一个进行copy，其他的通道进行affine。为了让每个通道都有被替换的机会，引入W矩阵，帮我们决定按什么样的顺序进行copy和affine，这种方法叫做1x1 convolution。1x1 convolution决定在每次仿射变换前对图片哪些区域进行像素对调，而copy和affine的顺序保持不变，这样和对调copy和affine的效果是一致的。

图2. 1x1 convolution

Glow中的一个flow包含如下子步骤：

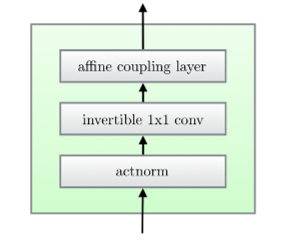
图3. One step of flow in the Glow model. (Image source: [Kingma and Dhariwal, 2018](https://arxiv.org/abs/1807.03039))

步骤1: Activation Normalization（actnorm）

类似于batch normalization，通过scale和bias参数进行仿射变换（和仿射耦合层不同的是不包含copy部分，而是对所有维度进行仿射变换），这些参数是可训练的。

步骤2: invertible 1x1 conv

图4. invertible 1x1 convolution

在每两个Glow flow之间，应用1x1卷积（卷积核的大小等于输入输出的channel数）可以产生channel顺序的任意排列，这样每个通道都有被替换的机会。

对于形状为 $h\times w \times c$ 的输入tensor $\mathbf{h}$，应用形状为 $c \times c$ 的可学习的1x1卷积权重矩阵 $\mathbf{W}$，得到的输出tensor为 $h\times w \times c$，用函数表示为 $f=\operatorname{conv2d}(\mathbf{h};\mathbf{W})$ 。为了应用变量变换规则，我们需要计算行列式 $|\operatorname{det}df/d\mathbf{h}|$的值，而通过推导可知可以直接通过计算矩阵 $\mathbf{W}$ 的行列式得到 $|\operatorname{det}df/d\mathbf{h}|$的值。计算过程如下：

1x1卷积的输入输出可以看做是 $h\times w$ 的矩阵， $\mathbf{x}_{ij} \in \mathbb{R}^c(i=1,\ldots,h,j=1,\ldots,w)$是矩阵中的一个数据点，和权重矩阵 $\mathbf{W}$ 相乘后得到对应的输出 $\mathbf{y}_{ij}\in \mathbb{R}^c(i=1,\ldots,h,j=1,\ldots,w)$,每个数据点的导数 $d\mathbf{x}_{ij}\mathbf{W}/d\mathbf{x}_{ij}=\mathbf{W}$, $h\times w$ 个数据点的行列式为：
$$
\operatorname{log}\left|\operatorname{det}\frac{\partial{\operatorname{conv2d}(\mathbf{h};\mathbf{W})}}{\partial\mathbf{h}} \right|=\operatorname{log}\left|\operatorname{det}\mathbf{W}^{h\times w}\right|={h \cdot w} \cdot \operatorname{log}\left|\operatorname{det}\mathbf{W}\right|
$$

因为 $\mathbf{W}$ 维度较小，所以 $\mathbf{W}$ 的行列式比较容易计算，1x1卷积的逆变换 $\mathbf{W}^{-1}$也比较容易计算，所以整体的计算量是可控的；

步骤3: 仿射对偶变换

这里的仿射对偶变换和RealNVP中的是一致的。

所以Glow的各个子步骤对应的逆函数和行列式计算如下所示：

图5. 各个子步骤对应的逆函数和行列式计算

疑问

为什么flow模型要求变换函数是可逆的？

这是normalizing flow进行密度估计的函数成立的条件；

Logan Liu's Blog